Moldings have always been the favorite of a finish carpenter.
For example when you trim a column, there's something about adding definition that makes the column better. It's like wrapping a present. The present itself is good but the wrapping and ribbons make it beautiful. It creates the anticipation and excitement of seeing it.
The way that the light breaks on a reveal or around a radius is what excites a carpenter . I believe it's important for a carpenter to appreciate his trim work. So often ,under the pressure of deadlines and financial constraints, a carpenter will feel un-appreciated, never takes a picture and moves on to the next job.
A trim carpenter needs to realize that the customer sees his work in much the same way as seeing a christmas tree loaded with wrapped presents.
The customer will always remember the first look and the memory of completion, a job well done.
The following writing about moldings is inspired by by Donald M. Rattner, Director of the Institute for the Study of Classical Architecture at the Real Estate Institute of New York University. He wrote an article in 'Traditional Building' about moldings that hit a chord with me.

The following is Donald Rattner's article re-written or with parts in whole.
When you understand moldings, you understand much about classical architecture -- the foundation of all traditional design.
click to enlarge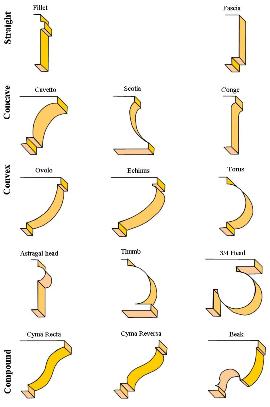
Shape is one way we classify moldings.
we first distinguish between Straight and Curved moldings.
In the straight group there are just two profiles: (1) FILLET, fillet is the term we give to a small, straight member,
(2)FASCIA,
fascia refers to a large flat profile.
The size distinction is relative; the size of a fillet could be large if you're talking about a molding on the exterior of a huge building, or small, if the fillet is part of a piece of cabinetry.

The classification of curved moldings is divided into three groups: they are
CONCAVE,
CONVEX,
and
COMPOUND.
In the Concave group are the
CAVETTO, which is roughly a quarter-circle;
the SCOTIA, which is actually a curve of greater rotation than a semi-circle;
and the CONG, which combines both straight and curved elements in one profile.
Next are the Convex moldings.
Those equaling or approximating a quarter-circle include the OVOLO, and the ECHINUS.
In the half-round class of convex moldings is the TORUS. A smaller version is called the ASTRAGAL HEAD.
Another relation is the THUMB. The TORUS is usually a full half-circle, while the THUMB is made up of radii of varying lengths. Moving from the semi-circular, we come to the THREE-QUARTER ROUND, sometimes known as theTHREE-QUARTER HEAD.

Compound moldings combine both concave and convex elements in a single molding.
The CYMA RECTA, from the Greek words for "wave" and "upright," is concave above and convex below. The reverse of this arrangement is the CYMA REVERSA.
The last is the BEAK molding -- the most complex of the profile types. The BEAK is formed from a variety of curved elements, and usually incorporates a chamfer, or diagonal cut.
Moldings are more than abstract geometric shapes.
An interesting concept that Donald Rattner puts forward is they are also what the architect uses to show the observer what the building is experiencing at a given point.

A moldings relationship to the building
A building is an object of considerable weight and channels that weight to the ground for dispersal. Thus certain portions of the building are subject to compressive stresses, much like the human being who has had a great weight on his shoulders.
Under the burden of such a weight the figure's normally upright silhouette is altered as a result of this weight. The weight of the building, or at least its sense of weight and mass, can be expressed through the application of its moldings in a manner representative of muscles flexed on the human figure.

The profiles used will depend on the intent of the stresses at that location. For instance, to direct force downward an inverted CYMA REVERSA might best convey the sense of gravity.
However, the release of weight at the top of a building could be expressed with a profile like the CYMA RECTA, a profile that forms a kind of canopy or sheltering effect appropriate to the top of a building.
Grouping by Function
Donald Rattner suggests that molding be regrouped according to their architectural function.

click to enlarge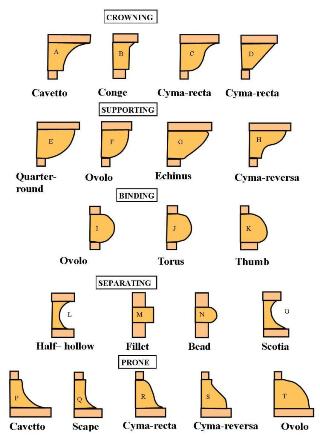

Under CROWNING are the moldings
CAVETTO,
CONGE,
and the CYMA RECTA, each of which ends in a concave curve.
Particularly appropriate and probably the most used for non-supporting situations is the CAVETTO, most of its section forms a concavity, depriving it of significant material strength and suggesting a conclusion.

The SUPPORTINGmoldings are the
QUARTER-ROUND, OVOLO,
ECHINUS,
and the CYMA REVERSA. These moldings suggest the ability to SUPPORT because the mass of their protruding section suggests they will hold up whatever is placed on top of them.
Other moldings imply the bearing of WEIGHT insofar as their bulging shapes imitate the deformations that occur when things are squashed.
BINDING moldings.
These profiles-
OVOLO
TORUS
and the THUMB
Are used to bind moldings to one another or to bind a panel to a molding. They will work well on top or bottom of any molding.
SEPARATING moldings are the
HALF–HOLLOW
FILLET
BEAD
and the SCOTIA
Think of them as the hollows and undulations between bulging muscles.

The PRONE moldings might better be described as TRANSITIVE types because they form graceful transitions from vertical surfaces to horizontal ones and at the same time, they suggest transfer of weight between two planes. The inverted CAVETTO, CONGE, and CYMAS fall into this last group.

Dramatizing Gravity Gravity is a primary contributor to the presence of stress inside an architectural construction. Nature acknowledges gravity's effect by detailing most living creatures differently at the bottom, middle, and top. The elements of classical architecture are organized into a clearly articulated base, middle section, and crown.

COntemporary and Classical
Contemporary architecture bases itself not on the imitation of natural phenomena, but on mimicking the inert or as is said in modernism, the machine. Take for example a cylinder, which, having no moldings or modeling is incapable of expressing the effect of gravity.
Contemporary theory accepts the geometry of architecture, but does away with nature.
Classicism, however, unites the two domains – the absolute qualities of pure mathematics and the figurative, changeable, and subjective tendencies of organic nature.
This dual aspect of classicism, Donald Rattner states, explains why people are so satisfied by the classical setting; it reflects their own nature as both emotional and rational beings.

The Function of Moldings
Like all elements of Architecture moldings perform both pragmatic and aesthetic functions.

But a base molding, for example, does more than just conceal a joint. First, it serves as a visual foot to the weight of the wall that rises above it; second, it MODULATES the transition between the vertical and horizontal planes of wall and floor; third, it PUNCTUATES the bottom of a wall to signal it has come to an end.
(PUNCTUATION is closely related to the term INFLECTION, which refers to the alteration of form, where one part is about to be transformed into another. Again, emulating most living organisms, the parts of a classical structure rarely change abruptly, but anticipate their change of condition by modifying themselves accordingly.)

The baseboard, together with the chair rail and cornice, serves the additional purpose of creating architecturally significant DIVISIONS OF SURFACE.
In turn, the size and scale of these and other moldings indicate SCALE, which can be loosely defined as the relationship between the human and architectural dimension. Size relates to scale, both in terms of the over-all dimensions of a molding series relative to the size of the space, and the degree to which the series itself is sub-divided. Generally, the more divisions within a given height, the smaller and more delicate the scale conveyed.
Moreover, moldings can help establish HIERARCHY by calling attention to prominent elements in a room, such as doors, windows, fireplace openings, and other apertures.
In these situations, they are often used to ARTICULATE STRUCTURE; the transition from a straight pier to a round arch, duly marked by a molding group called the IMPOST, and the detailing of the arch to express its tectonic role as a bent beam spanning an opening, are good examples of this aspect of moldings.

The impulse in classical design to frame things, to break down a surface into regularized compartments, is reflected in paneling. There, moldings help mediate the shift from one plane to another by lining the edges of the panel. And, of course, moldings furnish surfaces for ornamental embellishment.

Molding Design Let's look at some of the formal issues that can guide the design of moldings for interiors.

TYPE & SPECIMEN: First, we must distinguish between a general TYPE of molding and the potentially infinite number of individual SPECIMENS of a molding type that can be created by the designer. The distinction is an important reminder that classical design implies CREATIVE DIALOGUE between type and specimen, rule and invention -- and not simply the application of mechanical formulas.

ALTERNATION & CONTRAST: Moldings are rarely used singly; most often they are combined in a series. When using them in combination, there are several strategies available to enhance visual effect, resolve architectural problems, and avoid poor design.
For instance, one way to decide which moldings to use in a sequence is to seek out profiles that produce ALTERNATION and CONTRAST. The contrast may be between straight and curved. Or, the alternation could be between convex and concave profiles, e.g., a TORUS, followed by a SCOTIA, followed by another TORUS -- curve and counter-curve (center). We might even get contrast from the play of large and small: large CYMA RECTA, small CYMA REVERSA, etc.
REPETITION: Repetition can be successful in certain cases. In Fig 6 we have a convex ECHINUS followed by a convex bead, and the combination works perfectly well. But almost always you want to avoid the literal repetition of profiles one after the other.
click to enlarge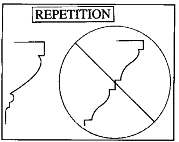

COORDINATION: In classical architecture, locating moldings relative to each other involves coordinating individual parts to make an ordered whole. This is usually attained by means of geometric alignments.
For instance, when a TORUS is set over a PLINTH, its outermost point is typically aligned with a vertical plane extended up from the face of the flat member. A vertical axis is then passed up through the geometric center of the TORUS to locate the tangent point of the half-round bead immediately above. In turn, another vertical axis from the center-point of the bead establishes the face of the fillet which sits upon the bead, and so on.
FACIAL ANGLE:
Another important alignment is the FACIAL ANGLE -- the incline off the vertical at which both individual moldings and molding groups will be pitched.
It's important to maintain a consistent facial angle throughout a molding sequence; otherwise the parts will appear disconnected because light will fall on them at unequal angles of incidence.
At various times in classical design, we find facial angles anywhere from 30 to 60 degrees. Differing explanations have been offered for these variations, such as the sharp angle of the sun in the Mediterranean climate requiring a steeper pitch for proper shadow effect.

PROPORTION & SCALE:
Both of these issues must be satisfied in molding design to achieve a harmonious whole, both in the relation of the profiles to their context, and to each other. The profiles on the left of the drawing are proportionate and internally well scaled,
the dominant CAVETTO clearly distinguished from the minor moldings. The same profiles on the right,however, reverse the major and minor in size. Consequently, the whole combination becomes confused and no longer a valid measure of scale, since there appears to be two different measures of scale at work.

REDUCTION/AMPLIFICATION:
While it's illogical to have two disparate scales present within a particular molding sequence, it's not unusual to have varying scales in moldings belonging to different features of the same building or space.
In structures of any complexity, one is often compelled to use moldings of diverse scales. The challenge is to adeptly bring about what I call the REDUCTION or AMPLIFICATION of scale where they meet.
In Fig. 10,
the TORUS and PLINTH moldings that articulate the base of the building are hefty in size and scale, because they are in proportion to the overall height of this very tall urban structure.
The moldings of the door surround, on the other hand, are literally reduced in size so they can relate to a more human scale appropriate for a door. Equally important is how they come together. Notice that the overall height of the step and pedestal element in the doorway is contained within the bottom flat member of the building's base, and how the greater number of divisions at the door element, versus the single division in the base, conveys the reduction in scale.
The same happens immediately above the big flat, where the height of just a single large TORUS is given over to both a TORUS and a PLINTH.

OCULAR RECTIFICATION:
Another instance where one might manipulate the size of profiles concerns the position of moldings relative to the eye. These revisions, known as OCULAR RECTIFICATIONS, are intended to restore the profile to its normal appearance by counteracting distortions inherent in human perception.
These distortions may be caused by such variables as the vantage point of the observer, available lighting, even the color of the moldings.
The issue of perspective is especially critical on the interior, where one rarely can stand as far back from a vertical surface as on the exterior.
To illustrate, in fig. 11 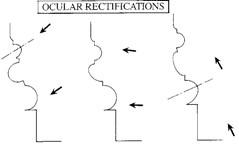if the profile stands roughly level with the eye, you would probably construct the various moldings according to regular geometry (center). But if this same sequence of profiles is to be located near the floor, you might make adjustments because the viewer will always be looking down on it.

For instance, you could re-configure the SCOTIA so more of it is visible, and less is concealed by the overhanging element. The face of the FILLETS may also be turned, and even the half-round could be given an egg-like contour to restore some of its underside to view (left).

LIGHT & SHADE:
Moldings on the outside of a building are almost always illuminated by direct sunlight. Interior moldings, on the other hand, are usually illuminated by indirect reflected light or electric lighting.
To compensate for the general weakness of interior light, you might want to make still more adjustments, since moldings only exist to the degree that they produce effective planes of light and shadow. This is especially crucial on the interior, where, in the absence of external miters, you must rely on the tonal play of shade and shadow to define the profiles at hand.

Space doesn't permit us to go into detail on the dynamics of light. We can make a few basic points, however, by comparing the OVOLO and ECHINUS profiles (upper left and middle right, fig. 12).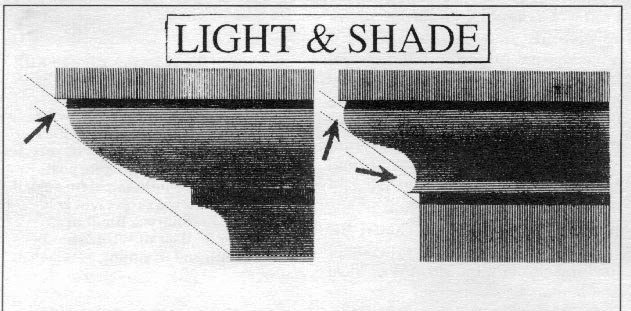
Assuming light falls in parallel rays from above, the gradation from light to dark on the OVOLO will occur in uniform increments because all points along its surface are equidistant from its geometric center. With the ECHINUS, the gradation is far more complex because it is constructed according to the non-circular geometry of the ellipse. An ellipse doesn't have geometric centers, and therefore -- unlike the OVOLO -- its curvature is constantly changing, making the shift from light to dark more subtle and less monotonous than the OVOLO.

Particularly noteworthy is the little highlight at the top of the ECHINUS, known as the QUIRKING, which is where a curve returns upon itself at its ends.
You can see it even more exaggerated in this CYMA REVERSA, (lower left of Fig. 11)

which can also be made from portions of an ellipse. The QUIRK can add much to a molding, in addition to the light effects it produces. For instance, it creates greater contrast between curved and straight at the extremes of a molding, in contrast to the OVOLO, where the profile assumes a vertical orientation just as it meets the adjacent fillet.
The QUIRK also anticipates and makes a more organic connection between contiguous elements than does the rather abrupt perpendicular termination of the OVOLO into the flat surface above.

CHARACTER:
The differing qualities of the ECHINUS and OVOLO brings us to the question of CHARACTER.
The option of selecting one molding over another, as well as the opportunity of manipulating a molding type, suggests a wide range of effects is available to the designer.
Compare the two different door casings in Fig. 13 .

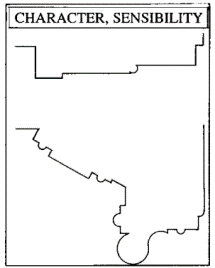
At the top is a design that comes from the 19th-century American design manual, BEAUTIES OF MODERN ARCHITECTURE. The bottom example is taken from a 17th-century Italian building. In terms of architectural character they could not be more dissimilar.
We have severity and simplicity versus elaboration and multiplicity; planar versus modeled; straight versus curved; orthogonal versus multi-directional; conventional versus occasionally non-conventional -- all of which could describe the respective architectural traditions from which these moldings derive.
Thus we come full circle back to an earlier statement about the classical system -- that one can find the spirit of the whole in the smallest part.

ABOUT THE AUTHOR Donald M. Rattner is a practicing architect and Director of The Institute for the Study of Classical Architecture (ISCA) at the Real Estate Institute of New York University.

ISCA organizes educational programs for professionals who wish to develop their skills in classical design. Programs include individual lectures, weekend seminars, and an intensive 6-week summer program. For more details, log onto ISCA's home page.

From Moldings to Woodworking tips